文章地址:https://ieeexplore.ieee.org/document/6848082
标题:Approximate multiple count in Wireless Sensor Networks
作者:Xiaolin Fang; Hong Gao; Jianzhong Li; Yingshu Li
发表会议:INFOCOM 2014
本文讲了无线传感网络(WSN, Wireless Sensor Networks)中的一类典型的 Aggregation 操作,即 Count 操作(以下有时也称为计数操作)。传统的Count操作仅仅支持一个属性,本文将count操作扩展到了多属性,并且提出了一种误差bounded by $hN/L$ 的算法,其中,$h$ 是routing tree的深度,$N$ 是items的总个数,$L$ 是网络带宽限制参数。同时本文也给出了带权重的计数方案。
下面是本文的笔记,序号和论文中的序号一样,有些地方我觉得对这篇文章的理解不重要,我跳过了,建议先看一下原文再来看我的笔记。
- 1 Introduction
- 2 Related Works
- 3 Problem Definition
- 4 Error Bounded Approximation Algorithm
- 5 Weighted Frequency Count Problem
- 6 Performance Evaluation
- 7 Conclusion
Introduction
在无线传感网络中,计数操作是一类经常用到的操作。何为计数呢,即告诉你某一类的数据一共有多少个。本文扩展了传统的问题场景,提出了multiple count问题,即一次返回多个数据类的计数结果,而不只是一个计数结果。
举个例子,比如物流监测,需要检测不同类型的商品有多少个。交通检测中,需要检测不同的交通工具的数量,如汽车多少个,自行车多少个等。在野外动物检测中,需要知道不同种类的动物有多少个等等。
所以可以设想一个这样的场景,我们以动物检测为例。假如在DPer家的大草原吧,很大很大的大草原。部署了好多个传感器,每个传感器可以知道它范围内鸡有多少个个,鸭有多少个,balabala。。。然后呢,传感器组成了一个树状结构,每个传感器收集到的数据会发送给自己的父节点,然后父节点把自己的数据和收到的所有子节点的数据求和,再发给自己的父节点,依次下去,最终得到一个所有数据的求和,在根节点上。我们通过根节点的数据就知道所有的数据啦。这个东西就叫做 routing tree,这个总结点呢,就叫 base station。
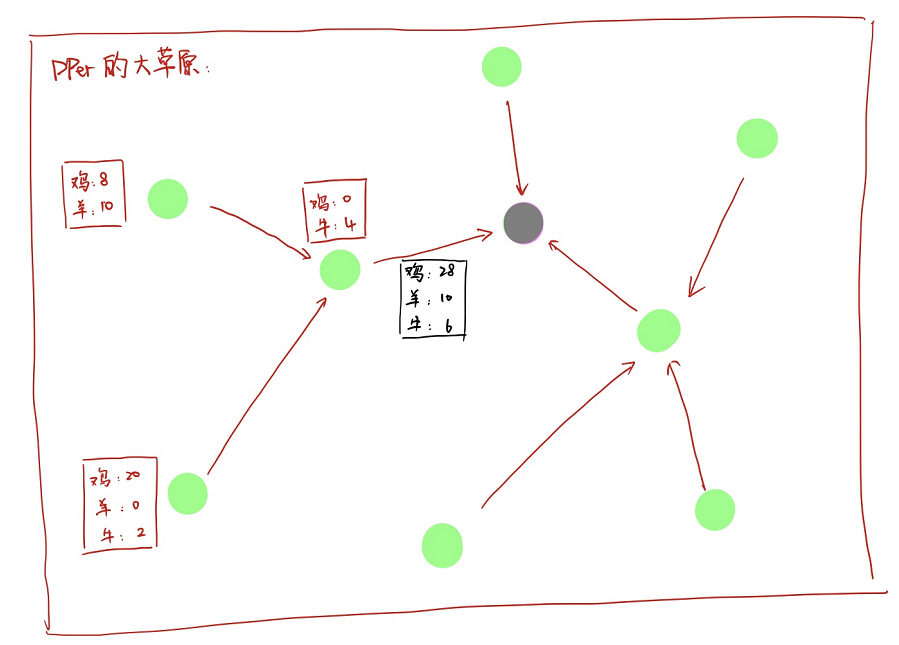
当然,这个问题还需要考虑到实际运用中的限制,本文考虑了两个实际中的限制:
- 在无线传感网络中,处于节能等balabala的需求,我们假定每个节点可以传输的包的数量是受限的。做这个的例子就是Telosb或Micaz motes一次可以传输的一个包的大小为28byte。也就是说,每个节点可以传输的数据信息是有限的,因此必要时候不得不抛弃一些东西,那必然导致误差。
- 有时候呢,不同的目标是有不同的权重的,所以如何处理权重也会影响实验结果喽。
总的来说呢,本文有以下几个贡献点:
- 就了解而言,这是第一篇在无线传感网络中做 multiple count problem 的。
- 给定网络限制 $L$,我们的算法误差是 bounded by $hN/L$ 的,其中 $h$ 是树深度,$N$ 是 item 的总数量。
- 本文也研究了带权重的 count multiple count problem。
- 仿真显示我们的结果很好,反正论文是人是鬼,贡献里面多有这么句话。
Related Works
这部分感觉和这个问题研究的具体的问题关联不大,相信写一大堆文字也没人看的。反正我是不会承认自己是因为懒才不写 related work的。
BTW,作为 INFOCOM 的文章,标题搞个 Related Works 真的好嘛,人家 Work 可是不可数的。
Problem Definition
现在我们来正式 formulate 本文中研究的问题。首先,我们假定有一个 routing tree。每个节点从自己的子节点收集数据,收集了所有子节点的数据之后把子节点数据和自己的数据求和之后发送给自己的父节点,直到所有的数据都到了 base station 那里。然后呢,我们还有两个假定:
- 每一个 item 的计数我们表示为:$[a_i, c_i]$,表示 $a_i$ 这个东西有 $c_i$ 个。
- 网络限制 $P$ 表示每个节点最多可以发送 $P$ 个包。
我们再假设每一个包可以放 $\lambda$ 个 item 的计数,如果我们假定一个节点收到的数据是 $\left\{\left[a_{1}, c_{1}\right],\left[a_{2}, c_{2}\right], \cdots,\left[a_{m}, c_{m}\right]\right\}$ 这样的话,如果 $m>\lambda P$ 呢,那么这个节点就需要丢弃掉一些数据了。幸运的是,有一些数据其实也是可以忍受的,比如交通识别中,我们只是想大致反应车流量,多一点少一点不重要。以及DPer的大草原中,我有100头羊,你告诉我我有80头,我也不 care,毕竟 DPer 可不是个穷人。
所以,假定对于某个item,经过我们的机制,我们就可以估计这个item有多少个,假如真实的count数是 $c$,估计的count结果是 $\hat{c}$,那么我们自然希望:
Error Bounded Approximation Algorithm
这个章节就是提出算法的章节了,再提出算法之前,作者先提出了一个 $block$ 的概念,为了方便,我们假定一个参数 $L=\frac{\lambda P-1}{2}$,这个 $L$ 接下来也会经常用到。那么什么是 $block$ 呢,定义如下:
A block is a set of item counts and the block size is no more than $L$.
作者为了解释 block,又多了一个 block size 的概念。block size 就是所有计数的和,举个例子,假如block $B = \left\{\left[a_{1}, c_{1}\right],\left[a_{2}, c_{2}\right], \cdots,\left[a_{m}, c_{m}\right]\right\}$,那么 我们需要满足:$\sum_{i=1}^{m} c_{i} \leq L$。
定义了什么是 block 之后,作者把 block 分为两类:完全block和不完全block。完全block就是说count计数总和刚好是$L$,反之则是不完全block。所以,接下来对于一个节点的所有数据呢,作者把这类数据分成了若干个完全block和一个非完全block。举个例子:
我们假定 $L=5$,用户的数据是 $D=\left\{\left[a_{1}, 4\right],\left[a_{2}, 3\right],\left[a_{3}, 2\right],\left[a_{4}, 1\right],\left[a_{5}, 1\right],\left[a_{6}, 1\right]\right\}$,那么可以分为两个完全块和一个非完全块,完全块 $B_{1}=\left\{\left[a_{1}, 4\right],\left[a_{2}, 1\right]\right\}$ 和 $B_{2}=\left\{\left[a_{2}, 2\right],\left[a_{3}, 2\right],\left[a_{4}, 1\right]\right\}$,以及非完全块 $B_{x}=\left\{\left[a_{5}, 1\right],\left[a_{6}, 1\right]\right\}$。画个图表示也就是:
计算得到完全块和非完全块的过程其实很简单,假定节点数据是 $D=\left\{\left[a_{1}, c_{1}\right],\left[a_{2}, c_{2}\right], \cdots,\left[a_{n}, c_{n}\right]\right\}$,那么有多少个完全块呢,有 $k=\left\lfloor\frac{\sum_{i=1}^{n} c_{i}}{L}\right\rfloor$,那么多个。同时,我们可以把完全块合到一起变成一个大的完全块,并用一个变量去表示有多少个完全块,比如前面的 $B_1, B_2$放到一起可以用 $B_r = B_1 \cup B_2 =\left\{\left[a_{1}, 4\right],\left[a_{2}, 3\right],\left[a_{3}, 2\right],\left[a_{4}, 1\right]\right\}$ ,再用 $k=2$ 表示$B_r$ 中包含2个完全块。根据这个思路,我们就有了一个DivideRemove算法,把数据分为完全块和非完全块。

那我们现在再来考虑带宽要求,每个节点发送的总数据是要在 $L$ 之内的,所以怎么办呢,作者很暴力,如果对于计数小于 $k$ 的,那么我们直接把对应的条目删掉。我们看看这样子的话,能达到要求吗?分析如下:
如果将计数小于 $k$ 的去掉,那么意味着在完全块中,最终上传的条目数量最大为 $k$ 的。又因为 $k=\left\lfloor\frac{\sum_{i=1}^{n} c_{i}}{L}\right\rfloor$,所以我们可以得到:
也就是说,每一个$B_r$ 中的item的数量是小于 $L$ 的。再换句话说就是 $B_r$ 中的元素个数是小于 $L$ 的。这个也就是文章中的定理1了。
我们注意到,每个节点上传的数据最终由三部分构成:$B_r, k, B_x$,经过刚才的分析我们知道 $\left|B_{r}\right| \leq L$,另一方面,很显然 $\left|B_{x}\right| \leq L$,所以,总的数据传输量为 :
也就是说,这个方法是满足网络带宽要求的。所以嘛,就有一个Remove操作了(这里也间接说明前面的 $L$ 为什么要取$(P\lambda - 1 ) / 2$)。算法如下:

好了,刚才一直考虑的都是一个节点对于自己数据的处理方式,那么我们注意了,实际上运行的过程中呢,对于中间的节点,他是需要对自己的子节点的数据进行求和的。所以呢,这个当中还有要个Merge,这个操作很简单不过了,就是把两个数据合并而已,直接看算法吧:

所以对于中间的节点来说呢,他需要把收集到的数据和自己的数据求和,然后再进行分块处理,这个算法思路其实就很清晰了,算法如下:

算法的第一行是把两个不完全块合并(Line 1-2),然后由不完全块合并形成的完全块需要和原有的完全块合并(Line 3-4),所以新的最终的完全块有三部分组成,为了达到前面的带宽要求,需要对合并的新的完全块进行Remove操作(Line 5),加上之前剩下的不完全块,就形成了这个节点的数据了。
提出了这个算法之后,自然免不了要进行一番分析。作者分析的结论是什么呢?是这样的:假定树的深度为 $h$,$N$ 是所有数据 count 的求和,即 $N=\sum c_{i}$,那么对于任意一类item,其求和的误差满足:
分析的过程论文中已经说的挺多的了,也就涉及对这个算法的分析,不涉及什么数学工具,可以直接参考原文章。
Weighted Frequency Count Problem
作者讲了不带权重的之后,又单独开了一章,引出一个新问题:如果有权重可咋办?
这是一个好问题,但是在作者的这个问题中实际上不是一个好问题,为什么呢,因为在这个背景下,权重没啥影响(但是在某些情况下,权重实际上是对误差会造成很大影响的,我们这里埋个伏笔,以后会有文章谈)。
我说没影响呢,是因为作者的处理方法很暴力,直接把权重乘以到原来的count结果上去,就over了。即每个用户的数据从 $[a_i, c_i]$ 变成了 $[a_i, p_i c_i]$ 这种类型,所以现在的误差是:
其中 $N=\sum p_{i} c_{i}$,由此可见,作者考虑权重和没考虑权重简直一模一样。
Performance Evaluation
接下来就到实验分析了,我最讨厌实验分析了-_-!。
作者分析了以下几个方面:
- $L$ 的变化对误差的影响(图2)
以这个为例简单分析一下把。首先这里的Error作者采用的是 relative error: $ \frac{c-\hat{c}}{N}$,加上之前提到的误差最大是 $hN / L$,所以上卖弄的灰色的就是理论上最大的误差了,也就是$h/L$。然后呢蓝色,白色和黑色是实验结果误差。
这里需要指出的是,relative error的定义有问题,作者所说的relative error实际上是absolute error除以 $N$,稍微思考一下的话其实会发现这个误差是很大很大的。而且这里把实际误差和理论上界误差拿来比较意义不大。后面的实验都比较类似,我就不一一讲了。
- $L$ 的变化对节点发送数据量的影响(图3)
- $L$ 的变化对内存使用量的影响
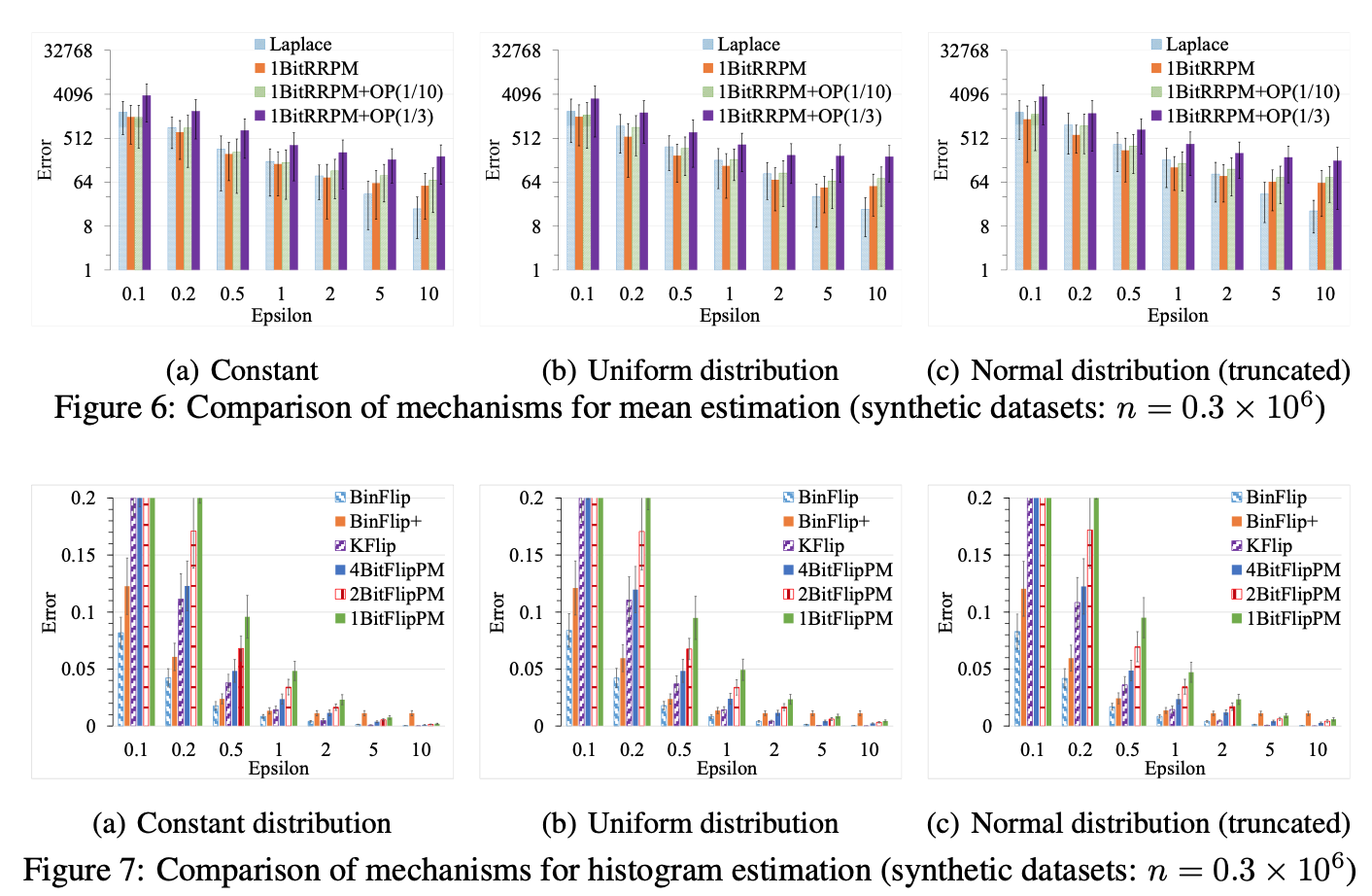
- $h$ 的变化对误差的影响(图5)
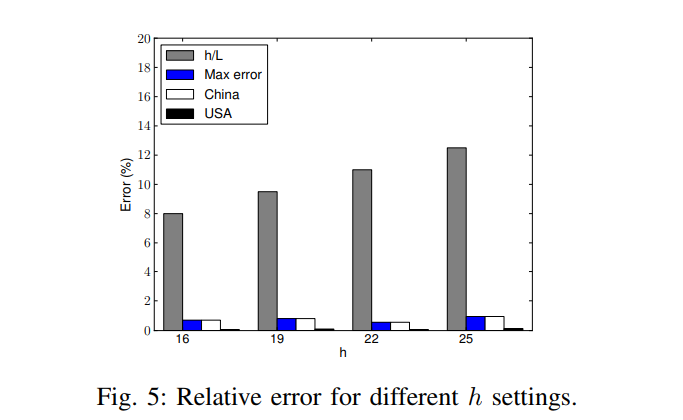
- $h$ 的变化对节点发送数据量的影响(图6)
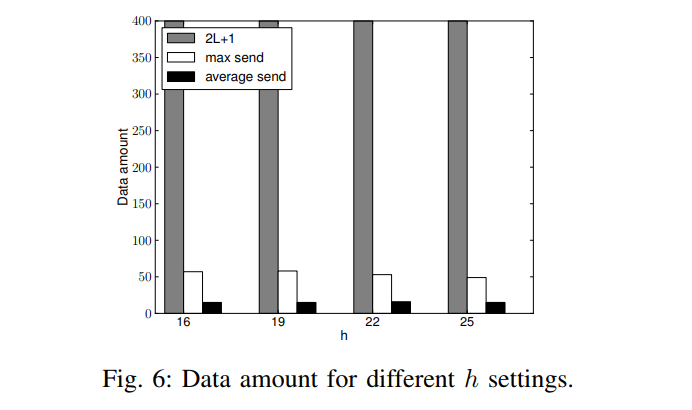
- $h$ 的变化对内存使用量的影响(图7)
- 换个数据集再来一遍实验(图8,9,10),这个我就不放图了。
本篇文章的实验分析比较简单,最主要的原因是什么呢,没有对比!比如给个误差说是10%,你也不好评价好坏。实际上,个人感觉因为会丢弃一些数据的关系,这个误差还是比较大的。
Conclusion
总结部分和摘要部分说的东西一样的,就不放上来了。
个人总结
这个文章读完有几个疑惑:
- 第一个困惑就是:我明白WSN中存在网络带宽限制,可是为什么带宽要用这种方法去表示啊,不应该是每个节点不管传输的数据是多大,都用一个int类型去表示吗,比如鸡有3只鸭有5只和鸡有4只鸭有20只所占用的带宽应该是一样的啊。但是在这个文章中,前者占用8,后者占用24。这点我实在难以理解。
- 为了达到带宽的要求,作者设计了丢包算法,但是显然丢包会带来误差。而且,这个包是不是丢的太多了?当然,这个改进的话就属于算法上的改进了。
- 看到啥文章都有个毛病,想想能不能搞个DP凑上去水个文章,那么这里面能不能加上DP的额外限制呢?如果要加的话,这里需要保护的对象是什么呢?
本篇内容到这里就结束了,欢迎关注公众号《差分隐私》,获取更多前沿技术。


